DiscreteGapStatistic estimates the number of clusters from (multiple choice) categorical response format data given any clustering algorithm extending the well-known gap statistic using a discrete distance based approach.
You can install the development version of DiscreteGapStatistic from GitHub with:
# install.packages("devtools")
devtools::install_github("ecortesgomez/DiscreteGapStatistic")Basic usage of DiscreteGapStatistic is shown using
likert’s Math Anxiety data.
library(DiscreteGapStatistic)
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, unionlibrary(ggplot2)Libraries are uploaded. Questions are lightly reformatted and the categories are shortened.
## mass dataset is loaded automatically with DiscreteGapStatistic
data(mass)
massSh <- mass[, -1]
sID <- substring(mass$Gender, 1, 1) ## Removing Gender variable
sID[sID == 'F'] <- paste0(sID[sID == 'F'], 1:sum(sID == 'F'))
sID[sID == 'M'] <- paste0(sID[sID == 'M'], 1:sum(sID == 'M'))
rownames(massSh) <- sID
Cats <- setNames(c('SD', 'D', 'N', 'A', 'SA'),
c('Strongly Disagree', 'Disagree', 'Neutral', 'Agree', 'Strongly Agree') )
massSh <- data.frame(apply(massSh, 2,
function(x) Cats[as.character(x)] %>%
factor(levels = Cats)),
check.names=FALSE, row.names = sID)
colnames(massSh) <- c('Q1: Math Interesting', 'Q2: Uptight Math Test',
'Q3: Use Math In Future', 'Q4: Mind Goes Blank', 'Q5: Math Relates to Life',
'Q6: Ability Solve Math Probls', 'Q7: Sinking Feeling', 'Q8: Math Challenging',
'Q9: Math Makes Me Nervous', 'Q10: Take More Math Classes',
'Q11: Math Makes Me Uneasy','Q12: Math Favorite Subj.',
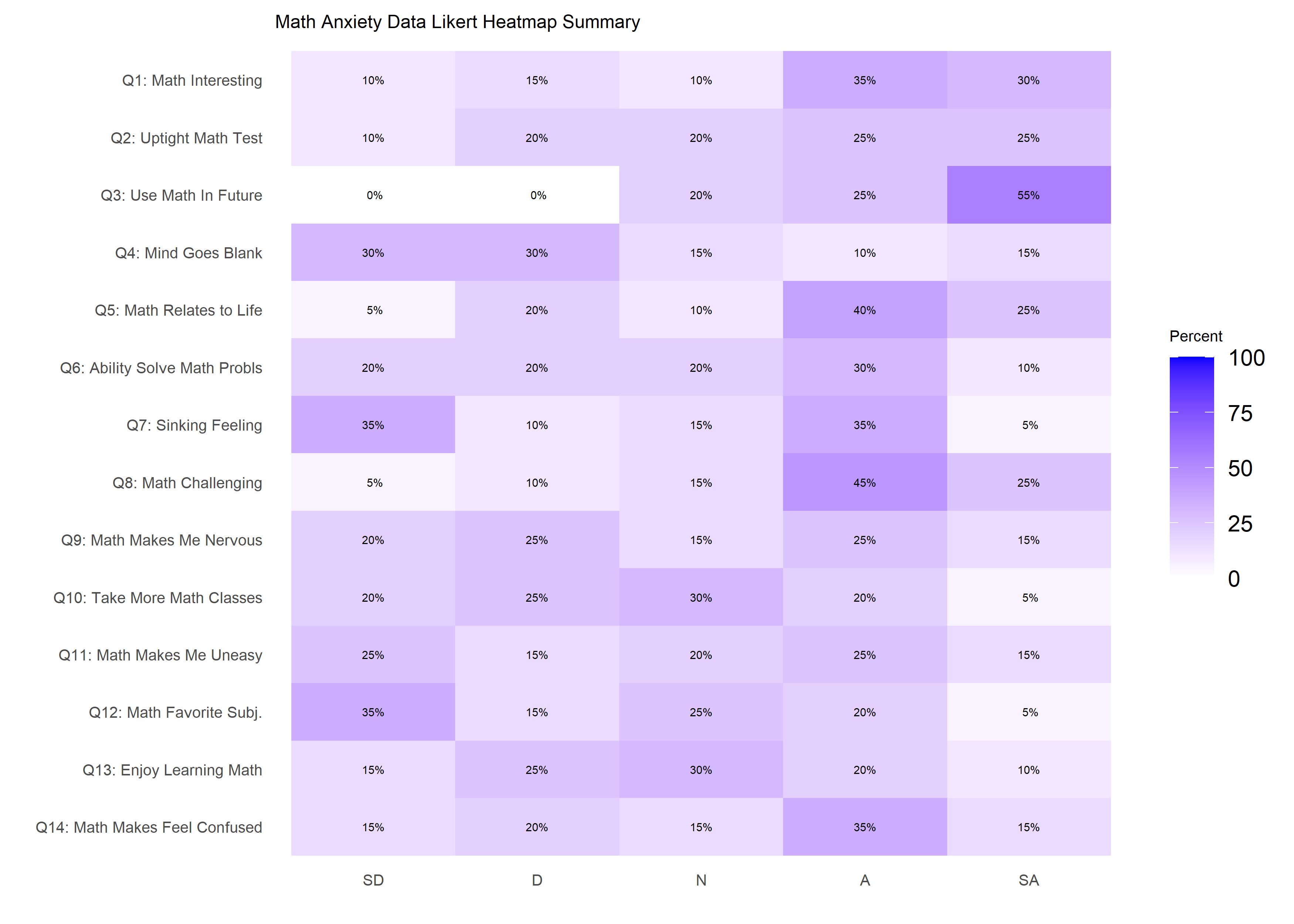
'Q13: Enjoy Learning Math', 'Q14: Math Makes Feel Confused')The dataset is visualized using a heatmap similar to the one produced
by likert::likert.heatmap.plot.
likert.heat.plot2(massSh,
allLevels = Cats,
text.size = 1.5)+
labs(title = 'Math Anxiety Data Likert Heatmap Summary')+
theme(axis.text = element_text(size = 6),
title = element_text(size = 6))
Five categorical distance functions are introduced to quantify
dissimilarities/discrepancies between two categorical vectors (see
function distancematrix). The following table describes the
available distances and the names used within the package.
#>
#> Attaching package: 'kableExtra'
#> The following object is masked from 'package:dplyr':
#>
#> group_rows| Distance | Name |
|---|---|
| Hamming | hamming |
| chi-square | chisquare |
| Cramer’s V | cramerV |
| Hellinger | hellinger |
| Bhattacharyya | bhattacharyya |
The resulting distance matrix from a rectangular dataset can easily
be displayed and organized using heatmaps. The following plots visualize
the massData using the defined distances with the function
distanceHeat. This function only requires the dataset
object and the name of the distance. It can also take advantage of the
options and functionalities available in the pheatmap
function (see the code below) from the pheatmap R package
[@kolde2019]. For
instance, by default, the columns are clustered using
clustering_method = 'complete' but this parameter can be
specified according to pheatmap’s options. Different
aesthetic options are exemplified in the plots below using the
introduced distances.
distanceHeat(x = massSh,
distName = 'hamming',
main = 'Hamming Distance\nMath Anxiety Data',
fontsize = 6.5)
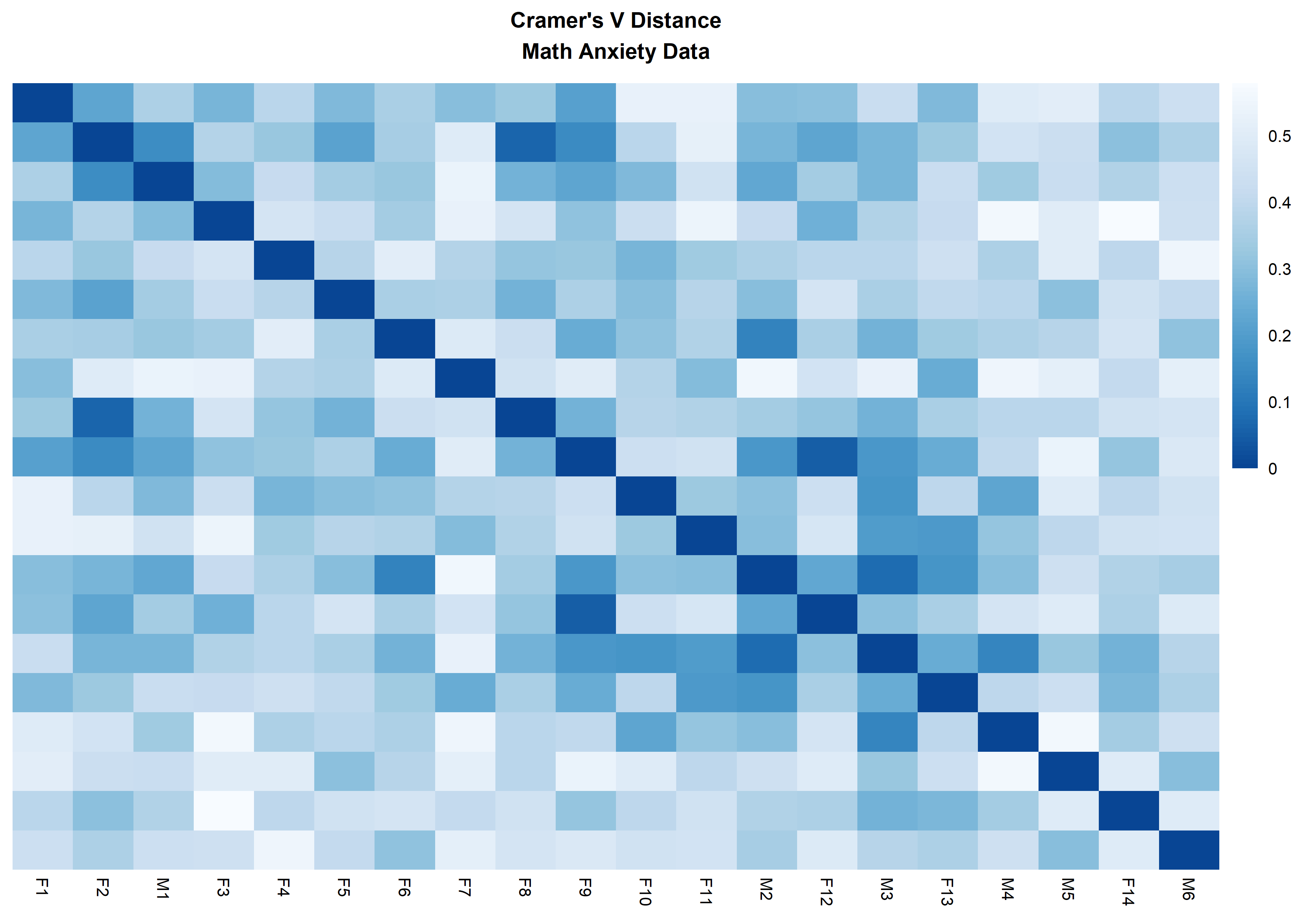
distanceHeat(x = massSh,
distName = 'cramerV',
main = "Cramer's V Distance\nMath Anxiety Data",
fontsize = 6.5,
show_rownames = FALSE,
cluster_rows = FALSE,
cluster_cols=FALSE)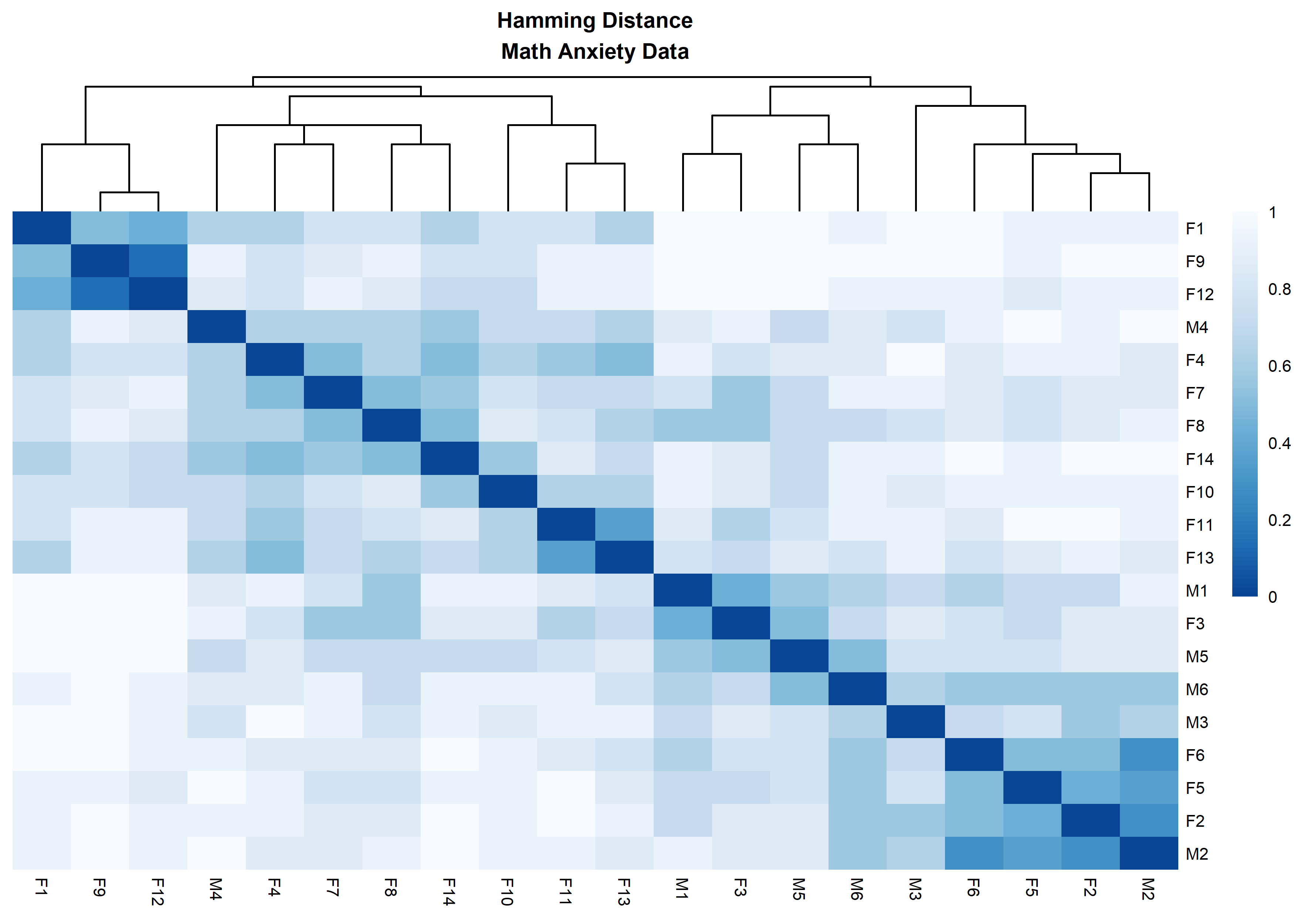
distanceHeat(x = massSh,
distName = 'hellinger',
main = 'Hellinger Distance\nMath Anxiety Data',
fontsize = 6.5,
show_rownames = TRUE,
border_color = 'black',
cluster_rows = FALSE,
cluster_cols=FALSE)
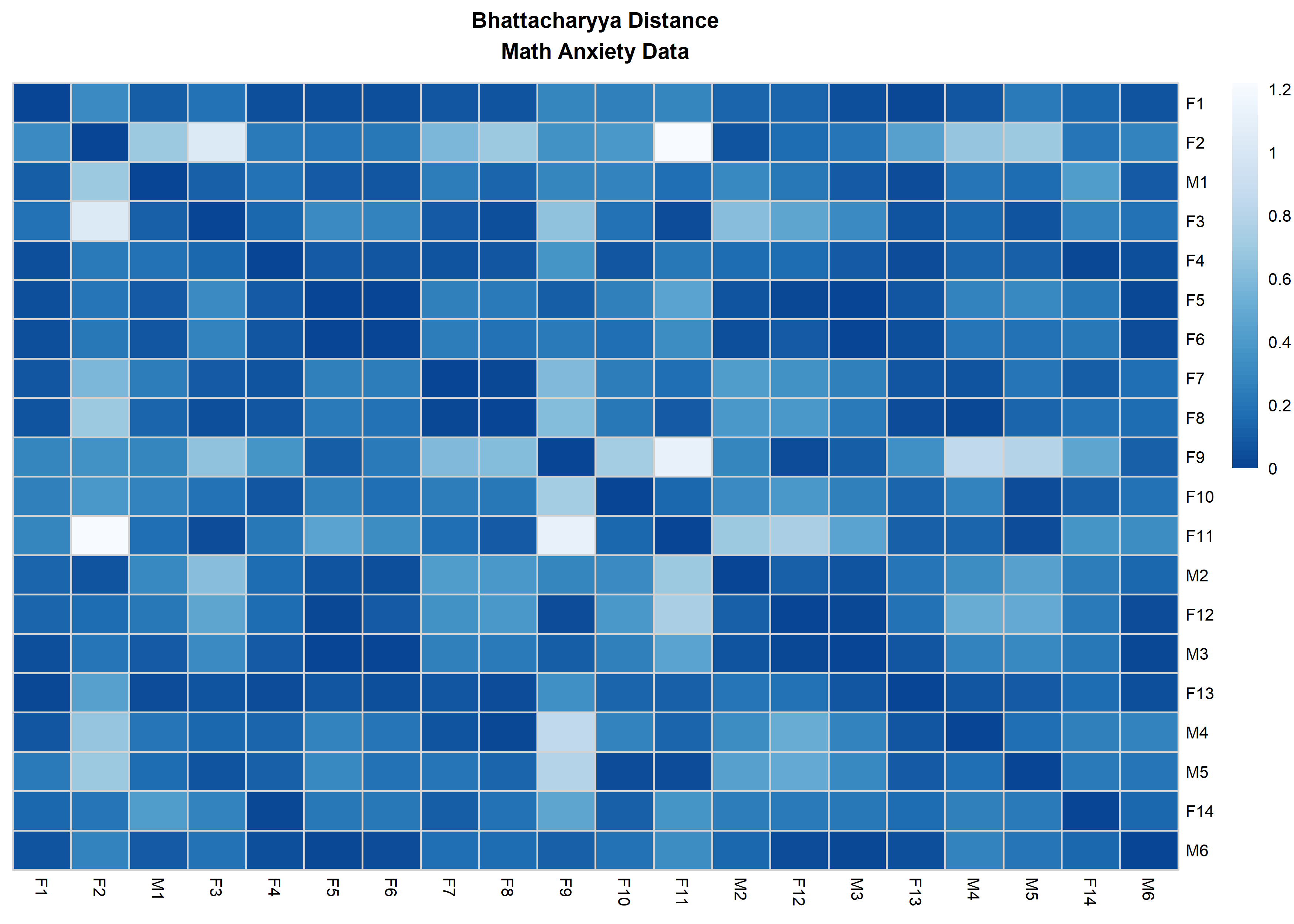
distanceHeat(x = massSh,
distName = 'bhattacharyya',
main = 'Bhattacharyya Distance\nMath Anxiety Data',
fontsize = 6.5,
show_rownames = TRUE,
border_color = 'lightgrey',
cluster_rows = FALSE,
cluster_cols=FALSE)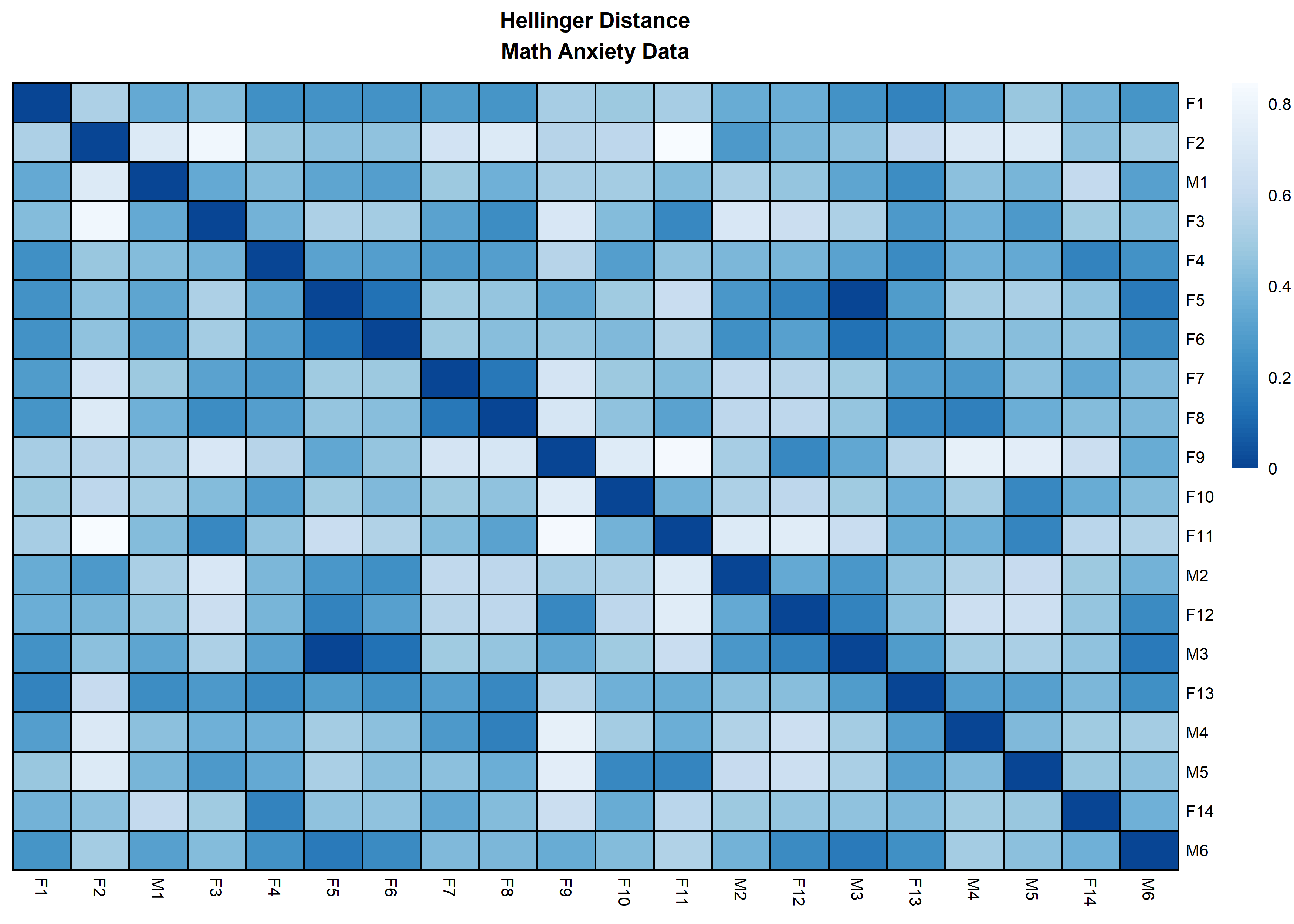
clusGapDiscr:
The Gap Statistic for discrete dataThe Gap Statistic (GS) in its original formulation by Tibshirani et.
al aims to determine an optimal number of clusters given a rectangular
dataset with continuous columns and a pre-specified clustering method
given \(k\) number of clusters
(i.e. \(k\)-means clustering or
partitioning around medoids (pam)). This is done by comparing the
within-cluster dispersion of the data to a randomly generated reference
null distribution of the data obtaining estimations via bootstrapping.
The idea is to quantify whether the clustering structure observed in the
data is considerably different compared to what would be expected by
random chance. clusGap is a widely used implementation of
the GS from the cluster package [@maechler2023cluster] with the
following basic arguments:
clusGap(x,
FUNcluster,
K.max,
B = 100,
verbose = interactive(),
...)x: argument can be data.frame or
matrix object where rows represent observations and columns
correspond to data features or variables. This matrix is expected to be
contain exclusively numerical input.FUNcluster: clustering function accepting on its first
argument a rectangular data object (like x) and a second
one specifying a desired k number of clusters.K.max: maximum number of clusters to consider.B: integer indicating the number of times to perform
the Montecarlo repetitions.The discrete GS (dGS) proposed applies and adapts the principle
behind the original formulation, but for categorical data using a
distance-based approach. The GS assumes that the distance between
observations can be correctly described with the Euclidean distance,
since it assumes the data is continuous. In the case of categorical
data, this distance assumption is not appropriate and a different class
of distances needs to be defined. clusGapDiscr is the main
function that performs and implements dGS. Parameters x,
K.max and B found in clusGapDiscr
have the same meaning and usage to the ones found in
clusGap. clusterFUN expects the name of a
well-known clustering algorithm implementation available in
R amenable to the proposed methodology. The input options
available for this parameter are the following:
| clusterFUN | Package |
|---|---|
| pam | cluster |
| fanny | cluster |
| diana | cluster |
| agnes-{average, single, complete, ward, weighted} | cluster |
| hclust-{average, single, complete, ward.D, ward.D2, mcquitty, median, centroid} | stats |
| kmodes-{1, 2, …, } | klaR |
The first four options are straight-forward since originally these
functions can output a clustering partition providing a distance matrix
and a given number of clusters. The following two implementations use a
flexible hierarchical clustering strategy. The number of desired
clusters can be obtained appropriately by cutting the resulting
hierarchical tree. This parameter requires the name of the
implementation and a dash (-) followed by the exact name of the
clustering strategy described in the package corresponding R package.
Lastly, a k-modes implementation is included using code found on
klaR with options fast=TRUE, weighted = FALSE.
The expected string after the dash is a non-negative integer specifying
the maximum number of iterations to carry out within the algorithm
(iter.max option; inputting kmodes alone runs
iter.max = 10 by default).
Additionally, the function requires a categorical distance from the list mentioned above. Another feature of the dGS is the reference null distribution used, which can be a discrete uniform distribution of the unique column-wise categories found in the data; this setting is defined as the Data Support (DS). In other settings, the categories to be used must be user-specified via a character vector or list. This setting will be referred as the Known Support (KS).
clusGapDiscr(x,
clusterFUN,
K.max,
B = nrow(x),
distName,
value.range = 'DS',
verbose = interactive(),
useLog = TRUE ...)distName: name of discrete distance. The available
options are 'hamming', 'chisquare',
'cramersV', 'bhattacharyya' and
'hellinger'.
value.range: specifies the values of the reference
null distribution. Possible values: 'DS' or a character
vector with unique values. 'DS' option extracts the unique
values found in x.
useLog: Binary truth variable specifying whether to
evaluate the Gap Statistic with or without \(log\) function.
Similar to clusGap, clusGapDiscr returns a
matrix object with K.max rows corresponding to the
user-specified number of clusters with an estimate of the GS and its
corresponding standard error. This information would then determine the
number of clusters according to the cluster-selection criterion. The one
used in DiscreteGapStatistic is the 1-SE criterion
implemented by the function findK, which accepts
clusGap objects. The following example applies the dGS on
the Math Anxiety data using the Hamming, \(\chi^2\), and Cramer’s V distances applying
the cluster::pam algorithm. A plot is then generated
displaying the dGS against the number of clusters. Each estimate is
accompanied by corresponding standard-error bars and a blue dashed line
indicating the chosen number of clusters.
The math anxiety data is further explored under different categorical
distances using the cluster::pam algorithm. The number of
bootstraps B is increased to 100 since the
sample size for this dataset is not too large. The maximum number of
clusters to consider is 9.
## Recall Cats:
# Cats <- setNames(object = c('SD', 'D', 'N', 'A', 'SA'),
# nm = c('Strongly Disagree', 'Disagree',
# 'Neutral',
# 'Agree', 'Strongly Agree') )
HammRun <- clusGapDiscr(x = massSh,
clusterFUN = 'pam',
B = 100,
K.max = 9,
value.range = 'DS',
distName = 'hamming')
#> Found levels: A, D, N, SA, SD
chisqRun <- clusGapDiscr(x = massSh,
clusterFUN = 'pam',
B = 100,
K.max = 9,
value.range = Cats,
distName = 'chisquare')
#> Found levels: A, D, N, SA, SD
crVRun <- clusGapDiscr(x = massSh,
clusterFUN = 'pam',
B = 100,
K.max = 9,
value.range = 'DS',
distName = 'cramerV')
#> Found levels: A, D, N, SA, SD
plot(HammRun,
main = "Discrete Gap statistic: Hamming Distance\nMath Anxiety Data",
cex = 2,
cex.lab=1.2,
cex.axis=1.5,
cex.main=1.5)
abline(v = findK(HammRun), lty=3, lwd=2, col="Blue")
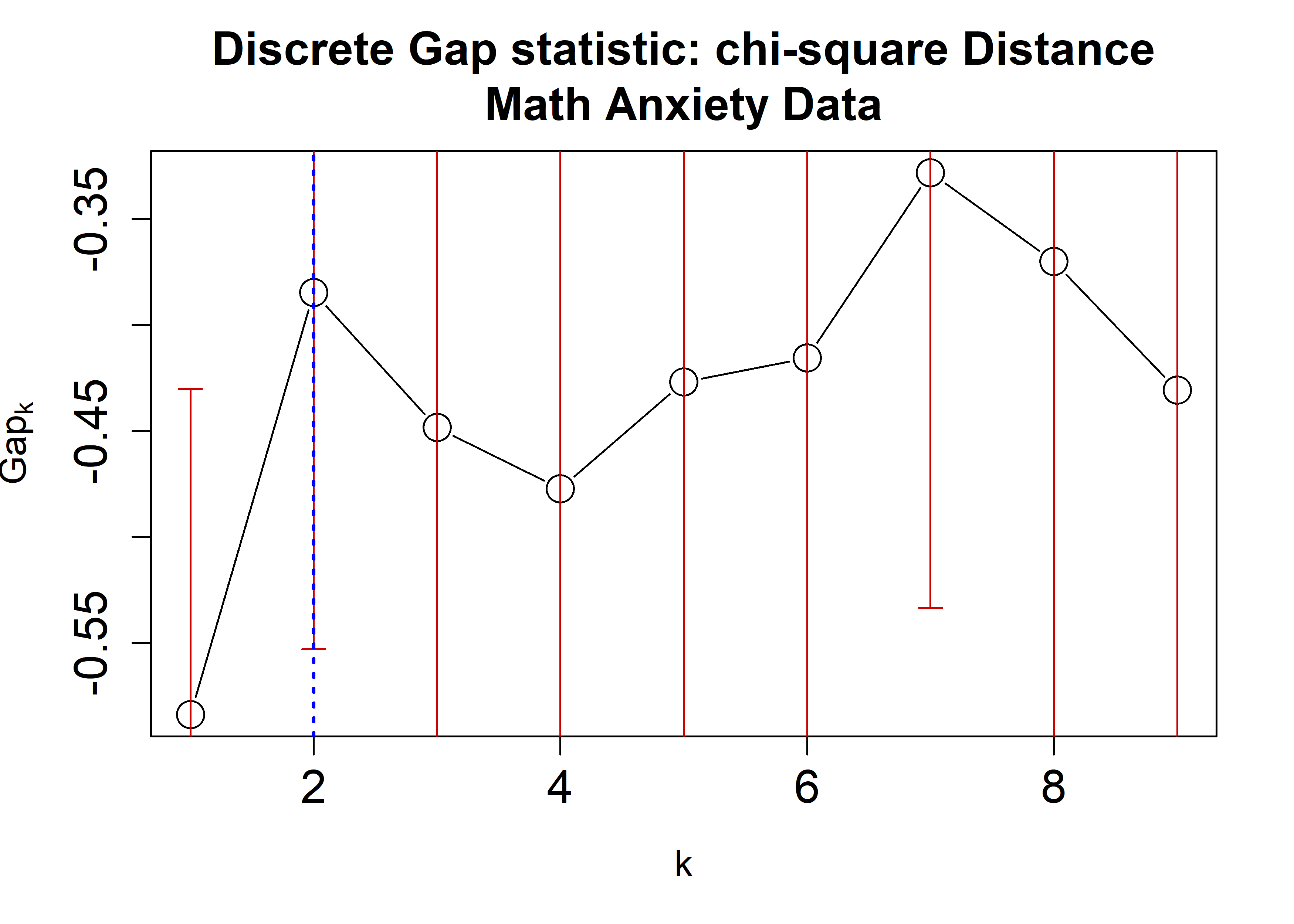
plot(chisqRun,
main = "Discrete Gap statistic: chi-square Distance\nMath Anxiety Data",
cex = 2,
cex.lab=1.2,
cex.axis=1.5,
cex.main=1.5)
abline(v = findK(chisqRun), lty=3, lwd=2, col="Blue")
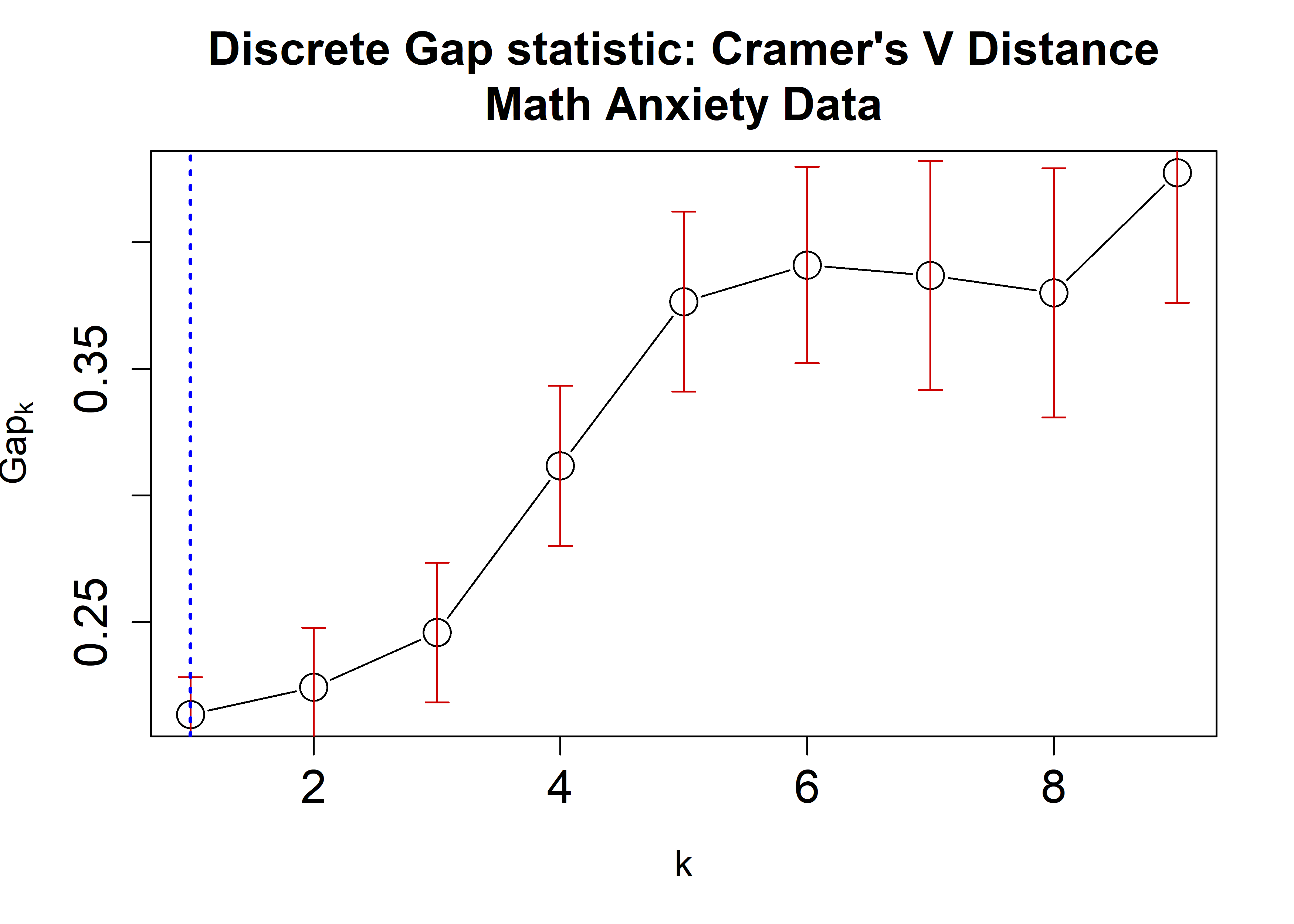
plot(crVRun,
main = "Discrete Gap statistic: Cramer's V Distance\nMath Anxiety Data",
cex = 2,
cex.lab=1.2,
cex.axis=1.5,
cex.main=1.5)
abline(v = findK(crVRun), lty=3, lwd=2, col="Blue")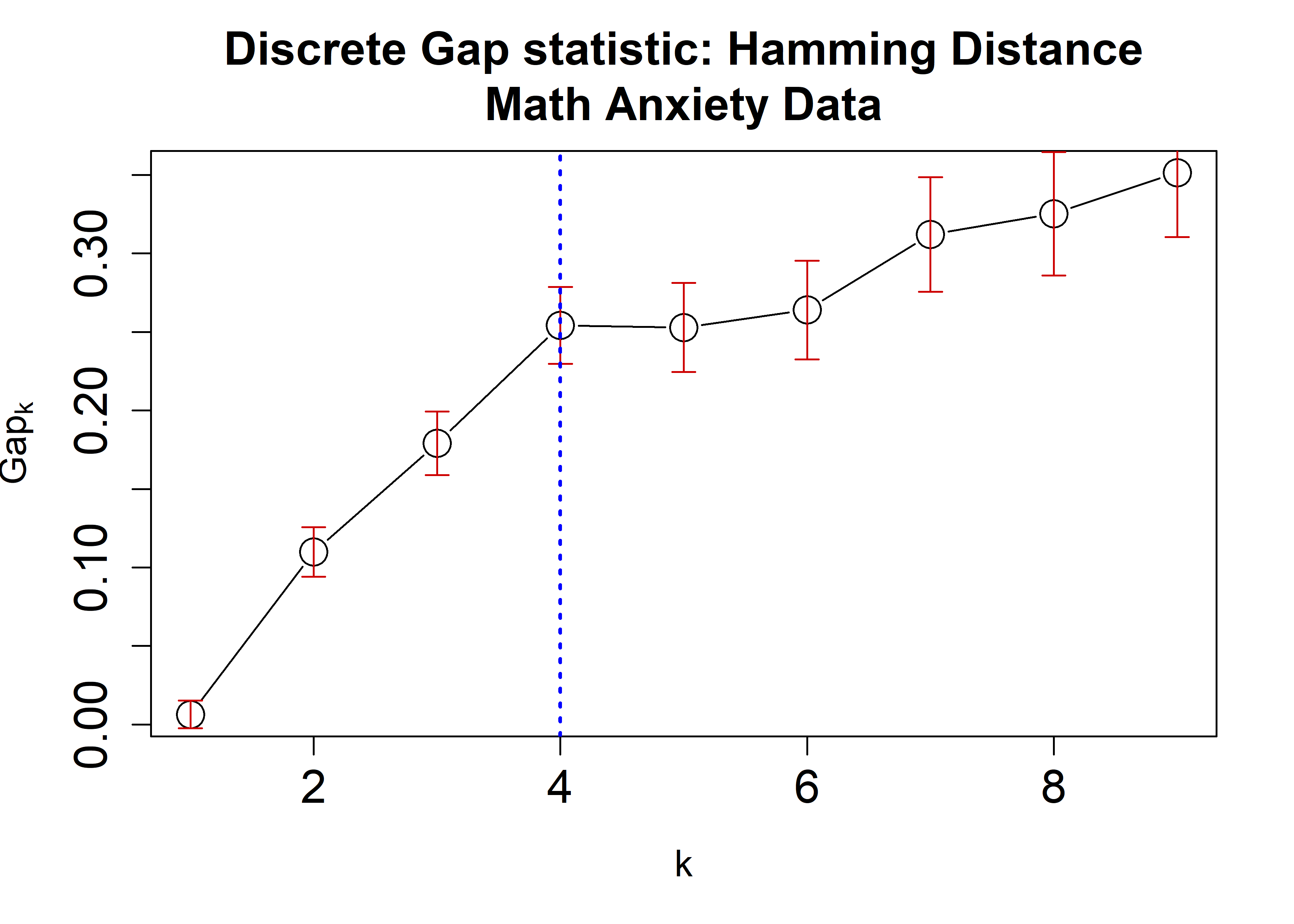
Notice that since all possible categorical values are available in
the data, using the option value.range = Cats would yield
exact same results.
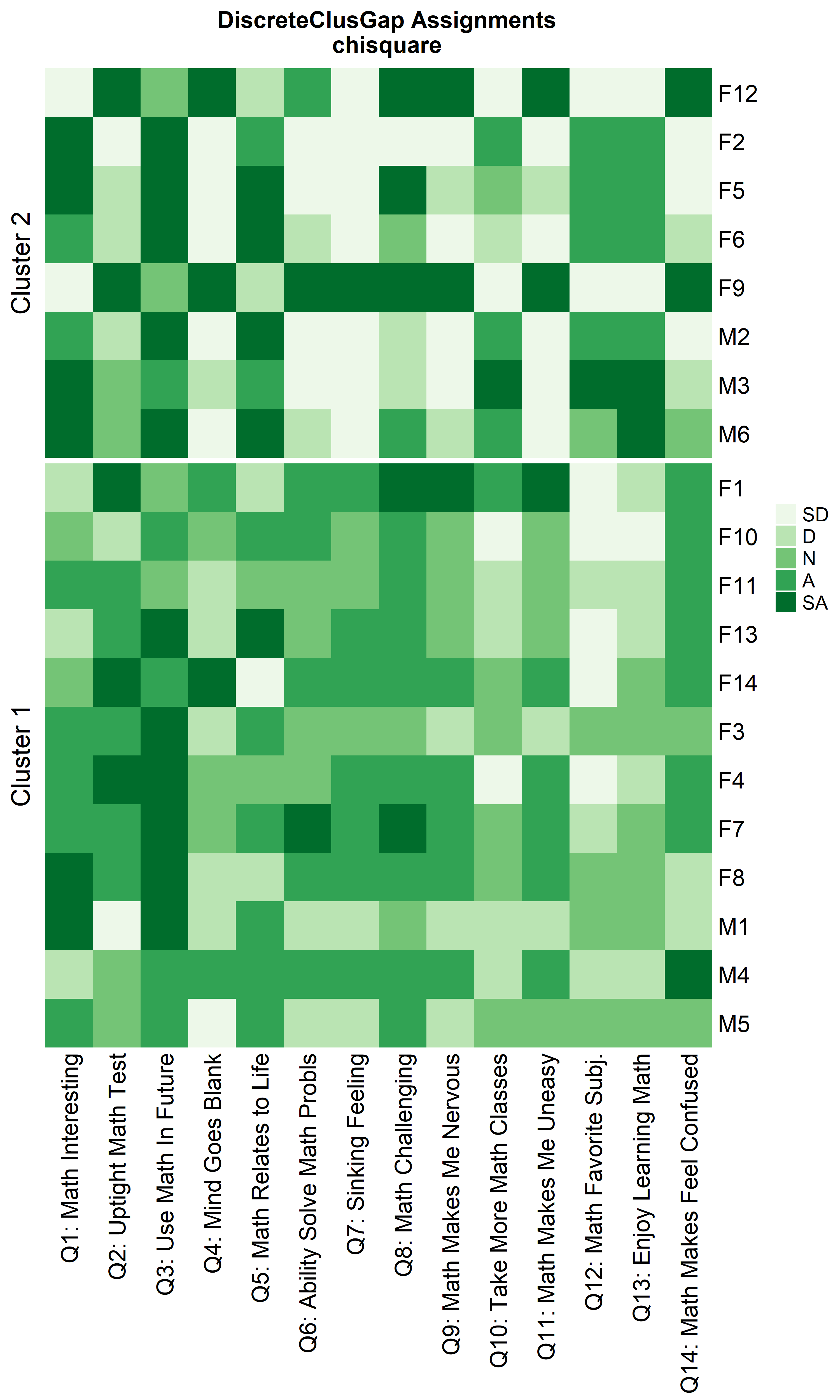
Heatmaps can be created to visualize the commonalities within each cluster and the differences between them.
ResHeatmap(x = massSh,
distName = 'hamming',
clusterFUN = 'pam',
catVals = Cats,
nCl = findK(HammRun),
out = 'heatmap',
prefObs = NULL, height = 6)
#> Warning: The input is a data frame-like object, convert it to a matrix.
#> Warning: Note: not all columns in the data frame are numeric. The data frame
#> will be converted into a character matrix.
ResHeatmap(x = massSh,
clusterFUN = 'pam',
distName = 'chisquare',
catVals = Cats,
nCl = findK(chisqRun),
out = 'heatmap',
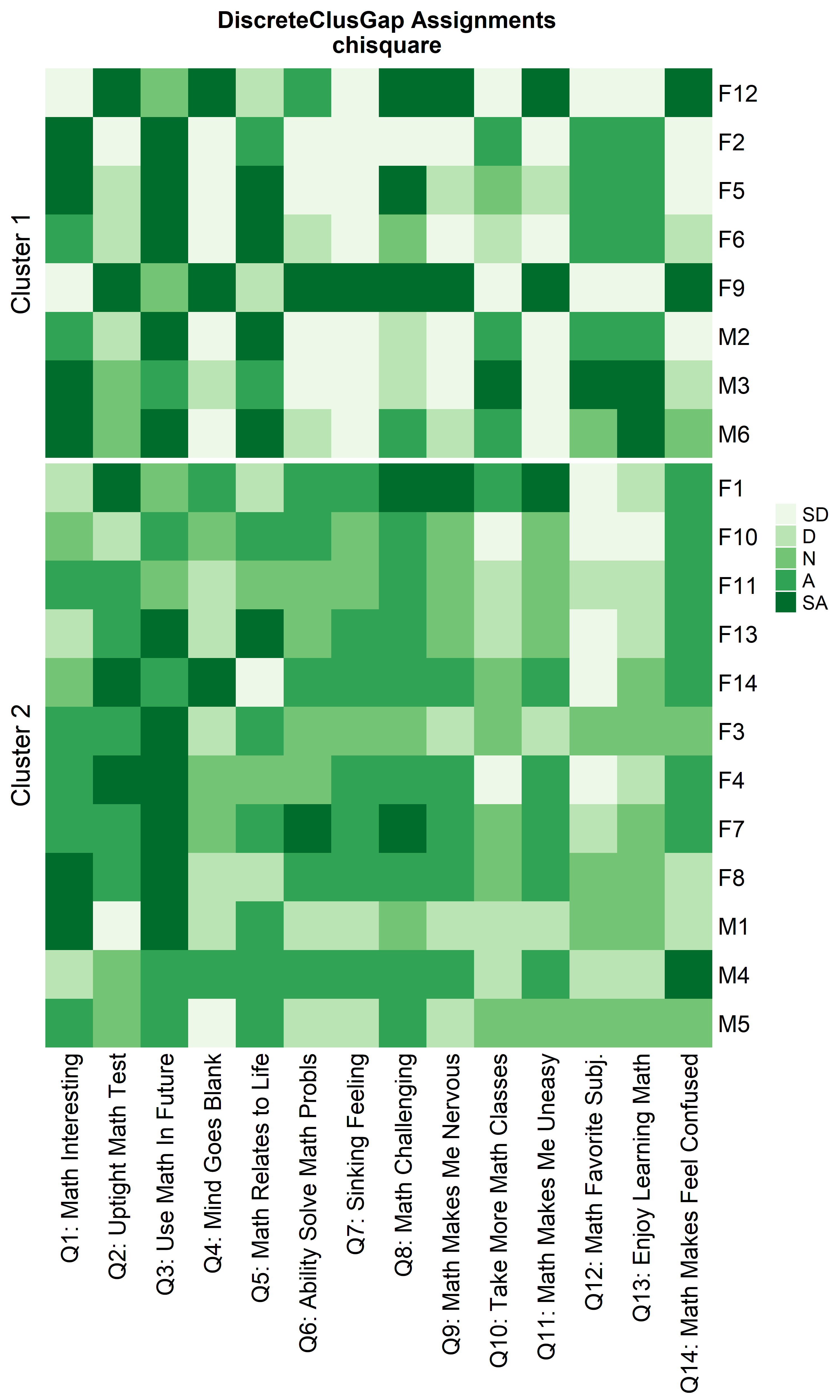
prefObs = NULL, height = 6)
#> Warning: The input is a data frame-like object, convert it to a matrix.
#> Warning: Note: not all columns in the data frame are numeric. The data frame
#> will be converted into a character matrix.
ResHeatmap(x = massSh,
clusterFUN = 'pam',
distName = 'cramerV',
catVals = Cats,
nCl = findK(crVRun),
out = 'heatmap',
prefObs = NULL, height = 6)
#> Warning: The input is a data frame-like object, convert it to a matrix.
#> Warning: Note: not all columns in the data frame are numeric. The data frame
#> will be converted into a character matrix.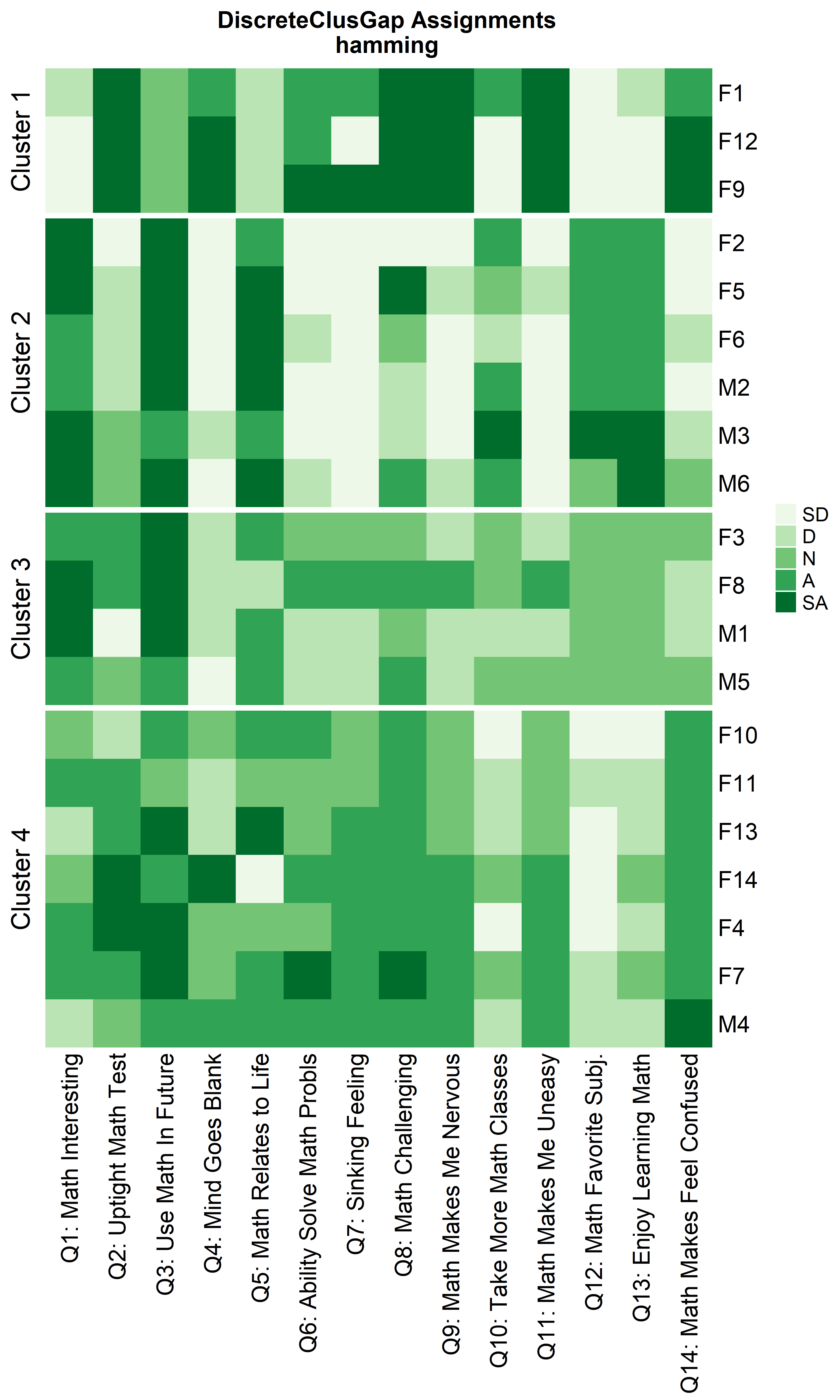
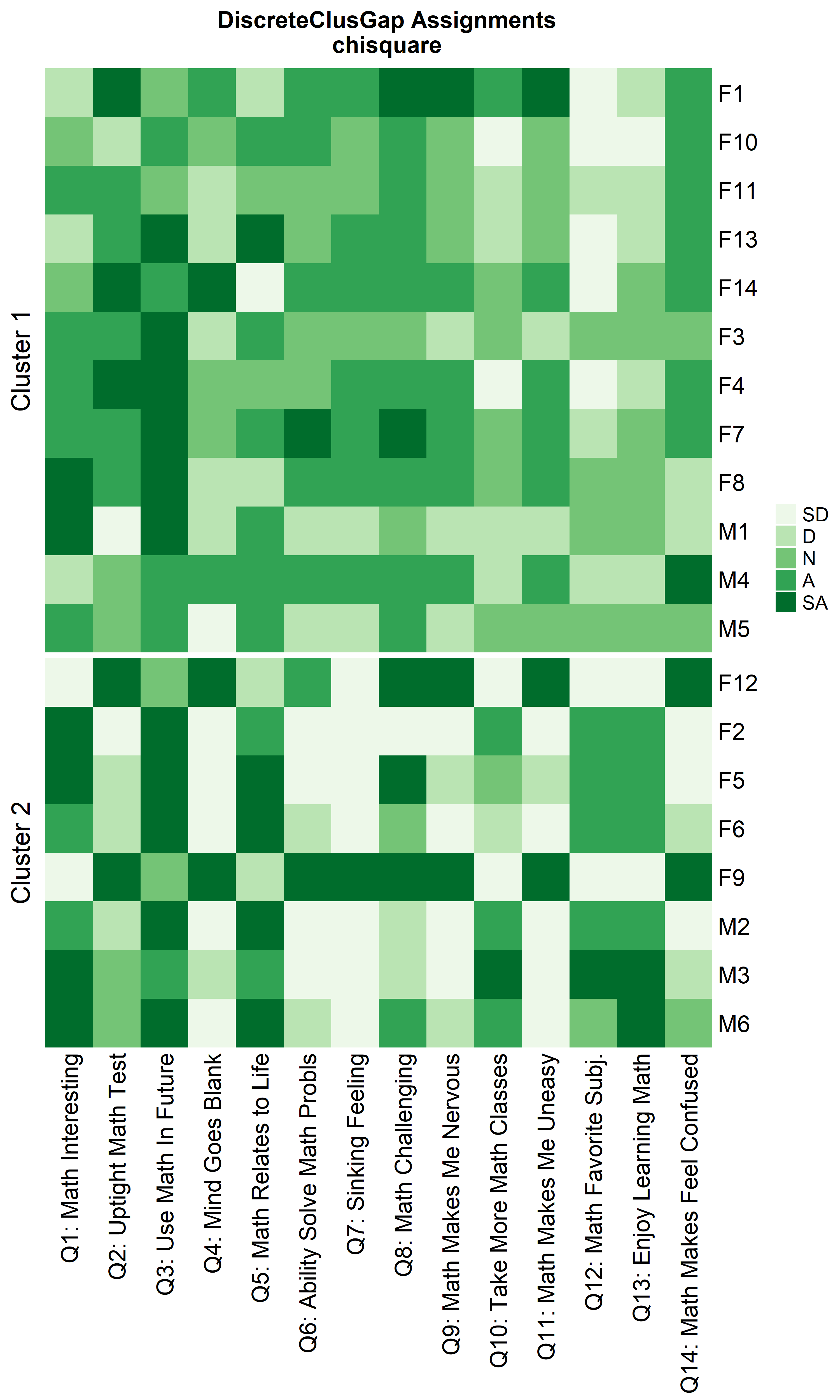
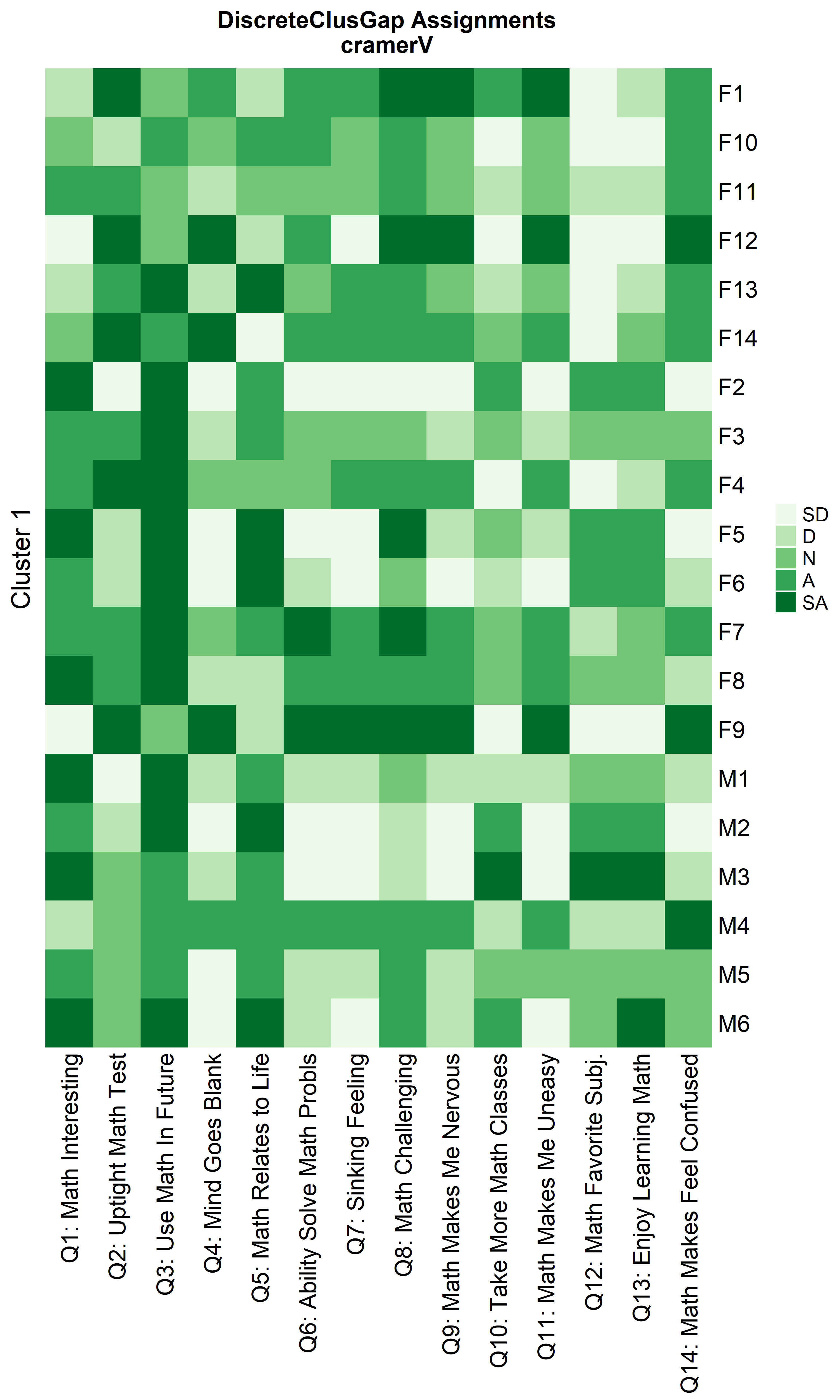
Notice that Hamming distance detects subclusters present in Cluster 2
from the \(\chi^2\) distance run. To
compare the similar clusters side-to-side, the parameter
nCl can be used to reorder the clusters relative to the
given ordering. This case nCl = 2:1 will alter (invert) the
order of the two clusters on the \(\chi^2\) based cluster. A third heatmap is
displayed relabeling the clusters from the \(\chi^2\) run using the
clusterNames = 'renumber' argument.
ResHeatmap(x = massSh,
clusterFUN = 'pam',
distName = 'hamming',
catVals = Cats,
nCl = findK(HammRun),
out = 'heatmap',
height = 6)
ResHeatmap(x = massSh,
clusterFUN = 'pam',
distName = 'chisquare',
catVals = Cats,
nCl = 2:1,
out = 'heatmap',
height = 6)
ResHeatmap(x = massSh,
clusterFUN = 'pam',
distName = 'chisquare',
catVals = Cats,
nCl = 2:1,
clusterNames = 'renumber',
out = 'heatmap',
height = 6)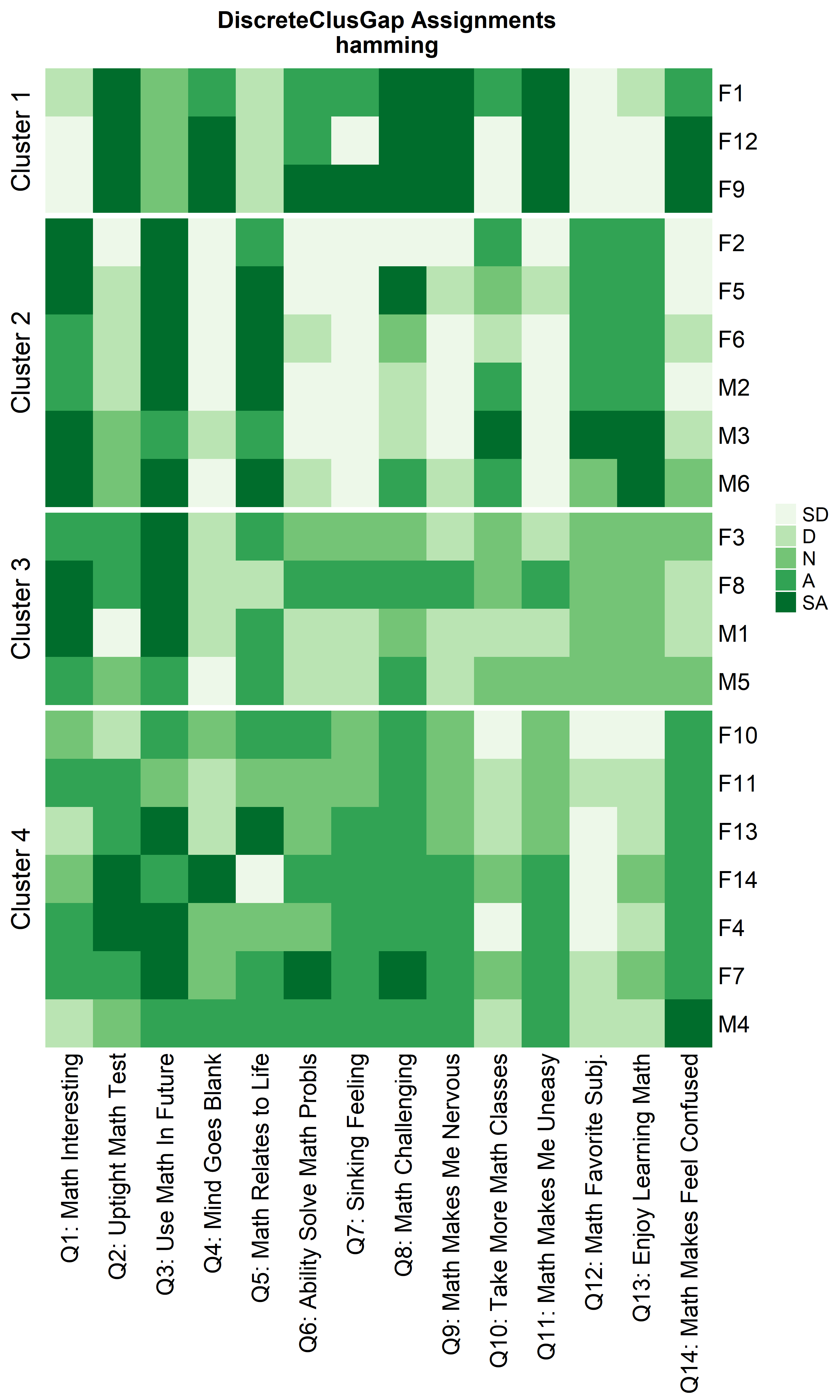
Other compatible clustering algorithms are considered additional to
cluster::pam only using the Hamming distance.
cluster algorithms: diana and
fanny
hDiaMa <- clusGapDiscr(massSh,
clusterFUN = 'diana',
K.max = 9,
B = 100)
ResHeatmap(x = massSh,
distName = 'hamming',
clusterFUN = 'diana',
catVals = Cats,
nCl = findK(hDiaMa),
out = 'heatmap',
height = 6)
hFanMa <- clusGapDiscr(massSh,
clusterFUN = 'fanny',
K.max = 9,
B = 100)
ResHeatmap(x = massSh,
clusterFUN = 'fanny',
distName = 'hamming',
catVals = Cats,
nCl = findK(hFanMa),
out = 'heatmap',
height = 6)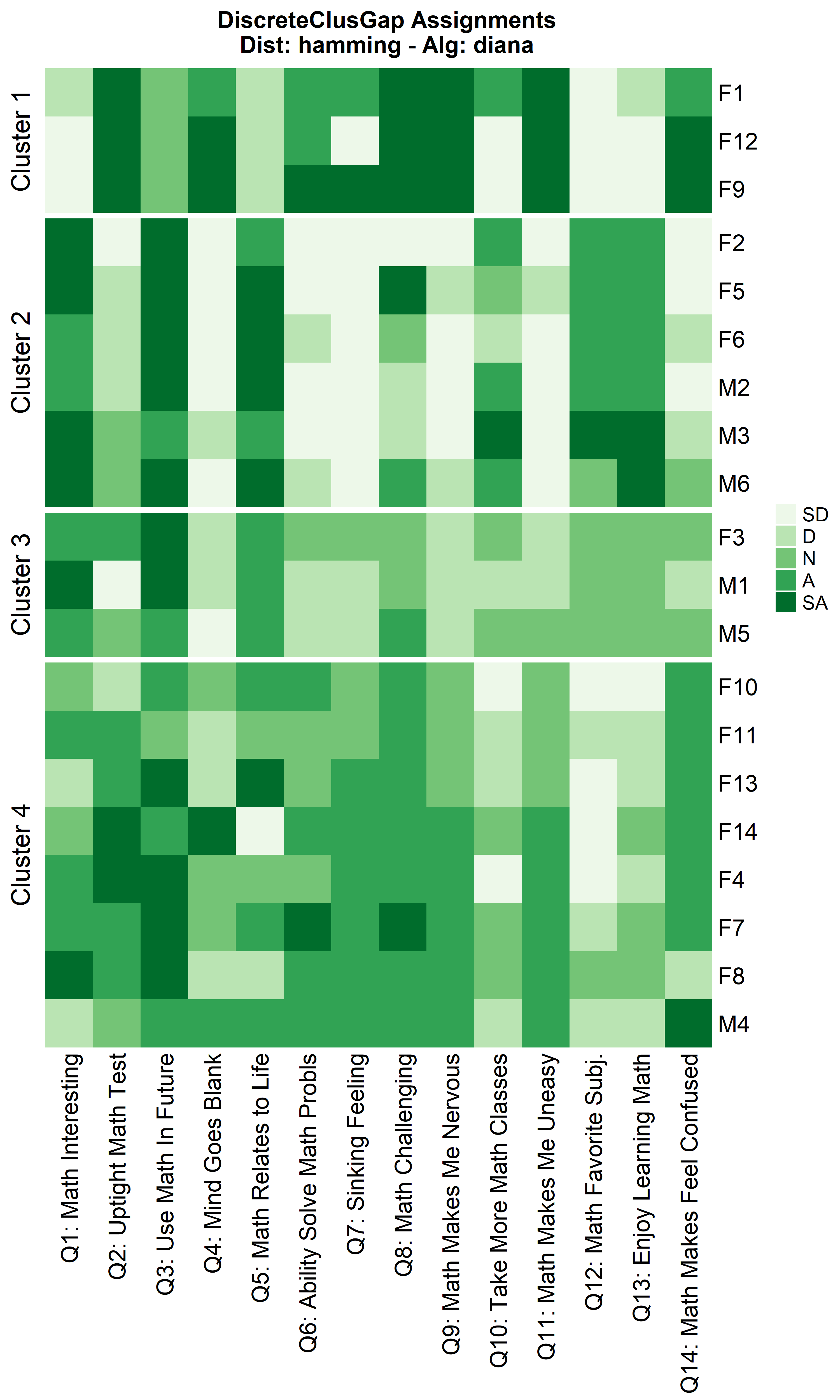

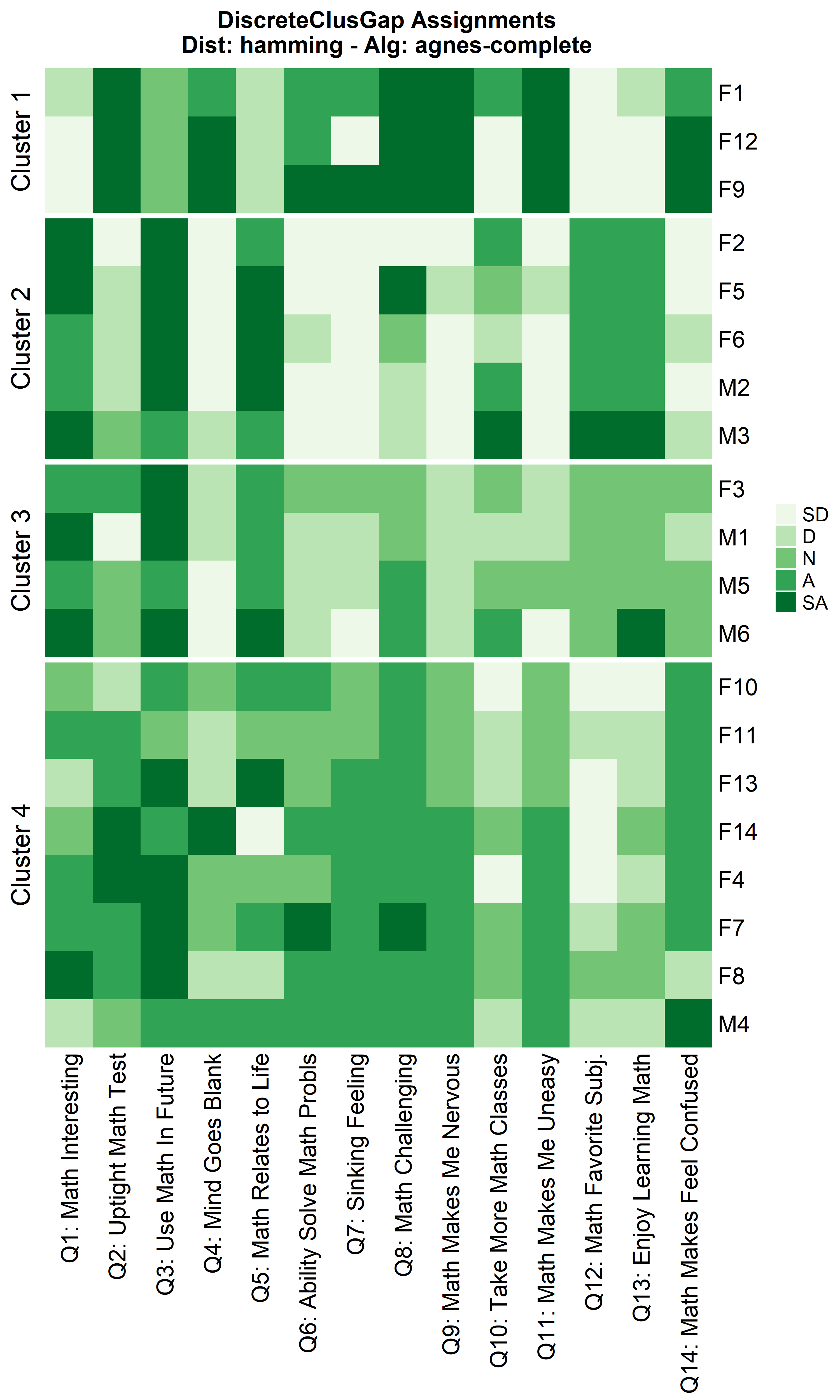
hAgnComMa <- clusGapDiscr(massSh,
clusterFUN = 'agnes-complete',
K.max = 9,
B = 100)
ResHeatmap(x = massSh,
distName = 'hamming',
clusterFUN = 'agnes-complete',
catVals = Cats,
nCl = findK(hAgnComMa),
out = 'heatmap',
height = 6)
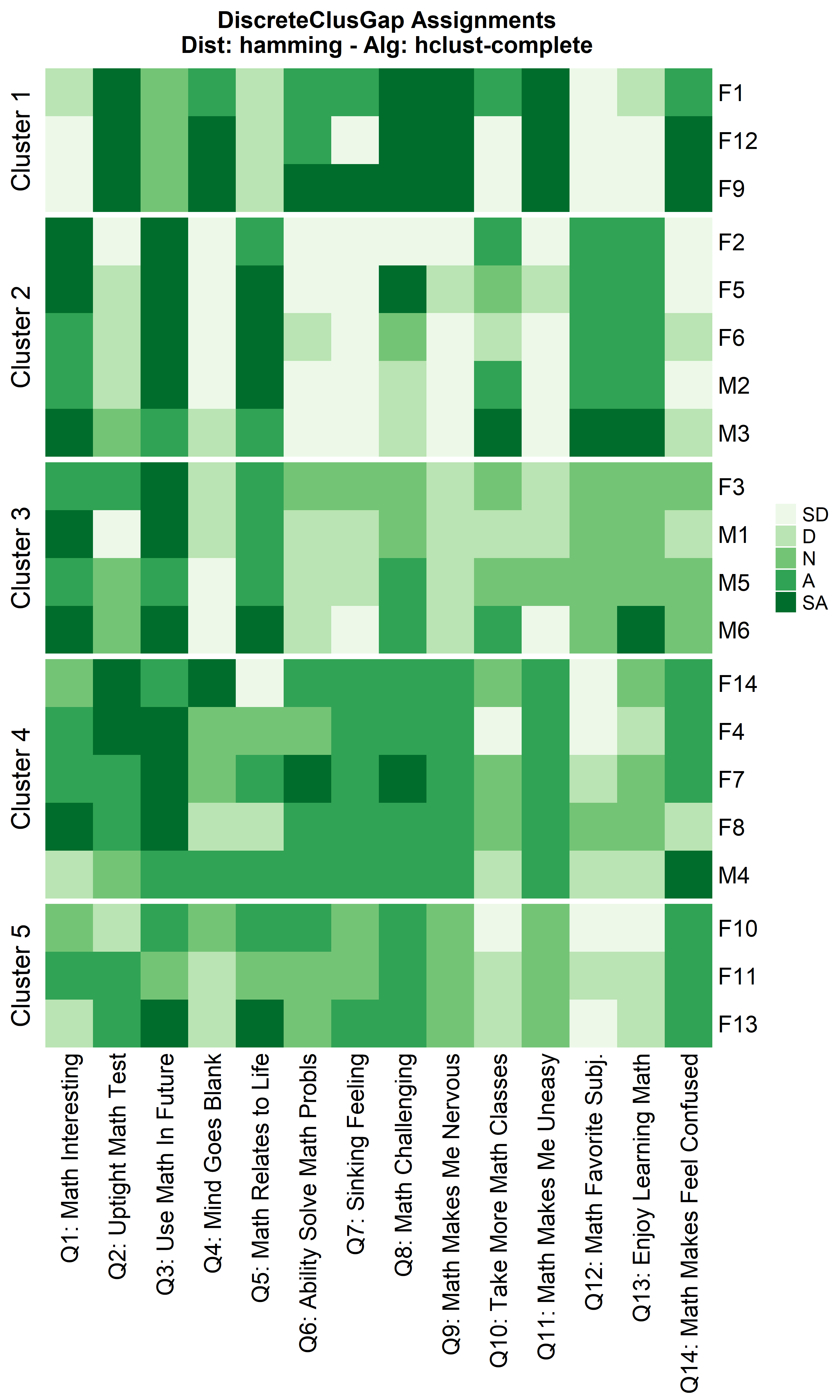
hhclComMa <- clusGapDiscr(massSh,
clusterFUN = 'hclust-complete',
K.max = 9,
B = 100)
ResHeatmap(x = massSh,
distName = 'hamming',
clusterFUN = 'hclust-complete',
catVals = Cats,
nCl = findK(hhclComMa),
out = 'heatmap',
height = 6)
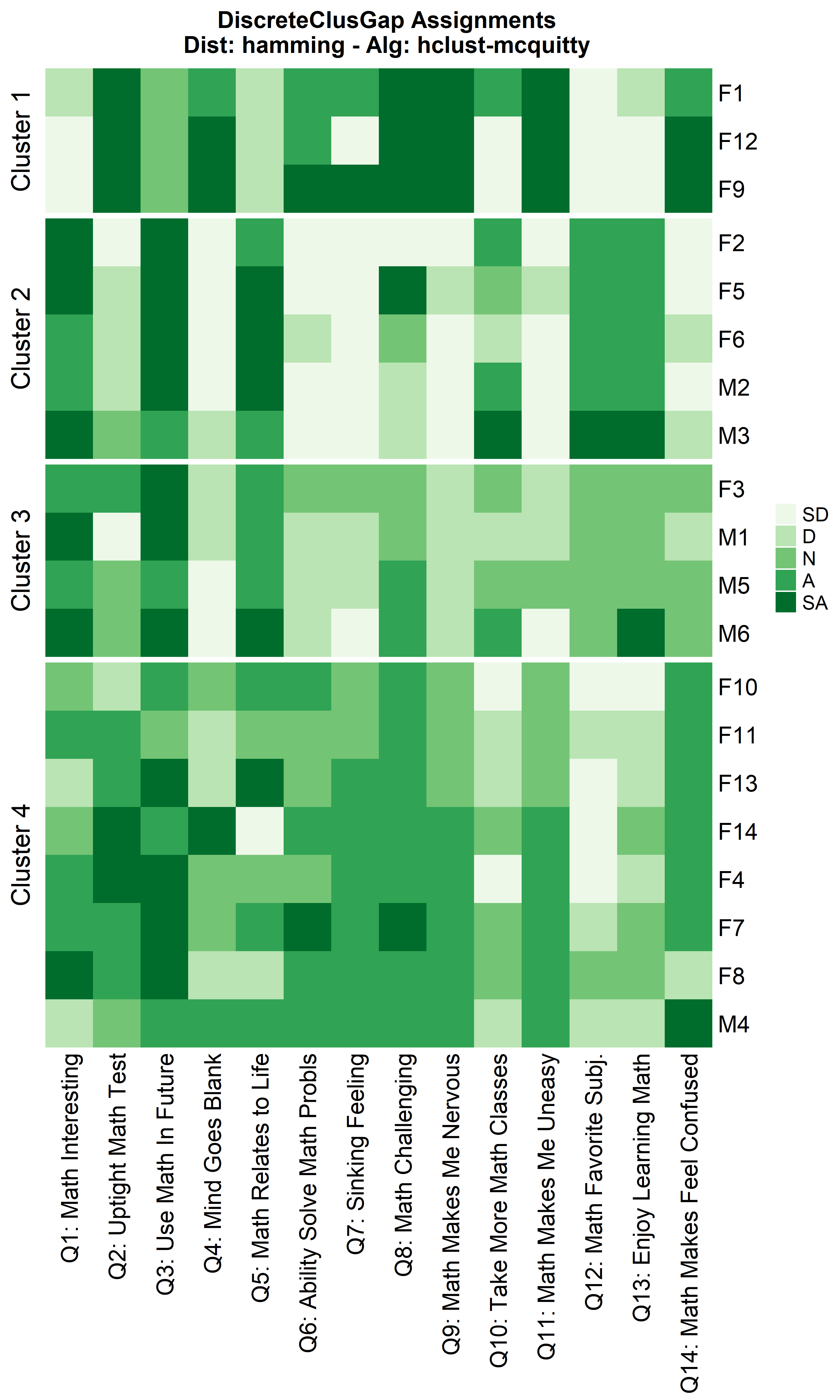
hhclMcqMa <- clusGapDiscr(massSh,
clusterFUN = 'hclust-mcquitty',
K.max = 9,
B = 100)
ResHeatmap(x = massSh,
distName = 'hamming',
clusterFUN = 'hclust-mcquitty',
catVals = Cats,
nCl = findK(hhclMcqMa),
out = 'heatmap',
height = 6)